作者 : wegx 随堂 · 三角函数与解三角形
收藏试卷 下载试卷 纯净版 派生 全部添加至试题篮
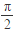 ②函数f(x)是偶函数
②函数f(x)是偶函数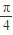 对称 ④函数f(x)在[
对称 ④函数f(x)在[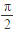 ,
,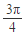 ]上为减函数
]上为减函数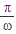 ]上( )
]上( )
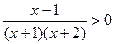 的解集为___________________
的解集为___________________
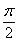 <α<β<
<α<β<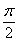 ,则2α-β的取值范围是________.
,则2α-β的取值范围是________.
 ,使
,使 ;②存在
;②存在 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点 对称.
对称.
 有两个不同的实数解,则实数a的取值范围是 .
有两个不同的实数解,则实数a的取值范围是 .
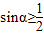 ,则角α的取值集合为 .
,则角α的取值集合为 .

 ,则其取最大值时x= .
,则其取最大值时x= .
 =0,则ω= .
=0,则ω= .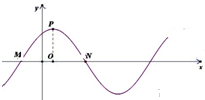
 ,则
,则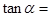 ___________。
___________。
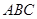 中,若
中,若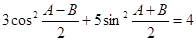 ,则
,则 ________.
________.
 ,则
,则 的值为________.
的值为________.
 ,则
,则 ______________
______________
 ,且
,且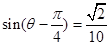 ,则
,则  ________.
________.
 ,
, ,则
,则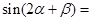 .
.
 的最大值为 。
的最大值为 。
 为锐角,若
为锐角,若 ,则
,则 的值为 .
的值为 .
 =
= ,则cos
,则cos =________.
=________.
 ,α是第二象限角,且tan(α+β)=1,则tan2β=________.
,α是第二象限角,且tan(α+β)=1,则tan2β=________.
 ,则tan(α+β)=________.
,则tan(α+β)=________.
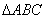 中,若
中,若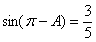 ,
,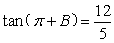 ,则
,则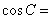
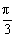 -x)+sin2(
-x)+sin2(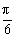 +x)=_________
+x)=_________
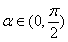 ,且
,且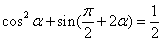 ,则
,则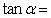 ____ ____.
____ ____.
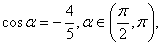 则
则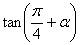 等于_________________.
等于_________________.
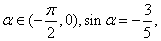 ,则
,则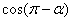 =___ ___.
=___ ___.
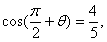 则
则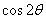 的值是________________.
的值是________________.
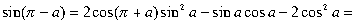 ______.
______.
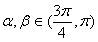 ,
,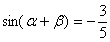 ,
,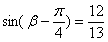 则
则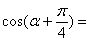 _____________.
_____________.
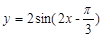 的图象关于点P
的图象关于点P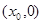 成中心对称,若
成中心对称,若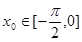 ,则
,则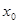 =________.
=________.
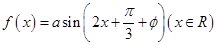 为偶函数,则
为偶函数,则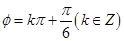 ;
;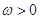 ,函数
,函数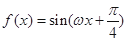 在
在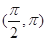 上单调递减,则
上单调递减,则 的取值范围是
的取值范围是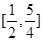 ;
;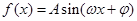 (其中
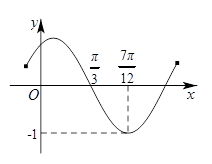
(其中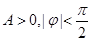 )的图象如图所示,则
)的图象如图所示,则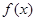 的解析式为
的解析式为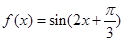 ;
;
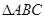 的内角
的内角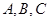 所对的边为
所对的边为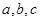 若
若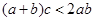 ,则
,则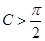 ;
;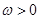 ,函数
,函数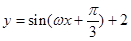 的图象向右平移
的图象向右平移 个单位后与原图象重合,则
个单位后与原图象重合,则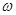 的最小值是
的最小值是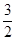 .
.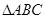 中,角
中,角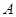 、
、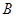 、
、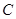 的对边分别为
的对边分别为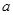 、
、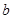 、
、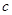 ,
,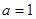 ,
,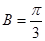 ,当
,当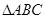 的面积等于
的面积等于 时,
时,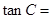 _______________.
_______________.
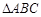 的三个内角
的三个内角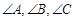 所对的边分别为
所对的边分别为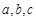 ,且
,且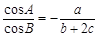 ,则角
,则角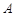 的大小为 .
的大小为 .
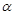 为锐角,若
为锐角,若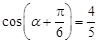 ,则
,则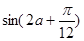 的值为
的值为
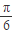 +x)=f(
+x)=f(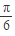 -x),则f(
-x),则f(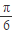 )= .
)= .
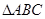 中,内角
中,内角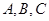 的对边分别为
的对边分别为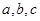 . 已知
. 已知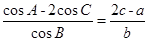 .
. 的值; (2) 若
的值; (2) 若 ,求
,求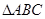 的面积.
的面积.
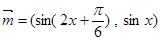 ,
,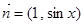 ,
,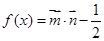 .
.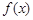 的单调递减区间;
的单调递减区间;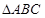 中,
中,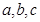 分别是角
分别是角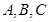 的对边,
的对边, ,
,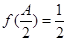 ,
,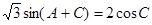 ,求
,求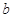 的大小.
的大小.
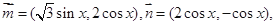 函数
函数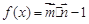 .
. 的最小正周期和对称轴的方程;
的最小正周期和对称轴的方程; 的角
的角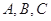 的对边分别为
的对边分别为 ,且
,且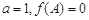 ,求
,求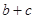 的取值范围.
的取值范围.
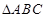 中,
中,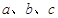 分别为角
分别为角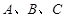 的对边,△ABC的面积S满足
的对边,△ABC的面积S满足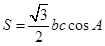 .
.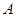 的值;
的值; ,设角
,设角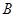 的大小为
的大小为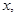 用
用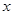 表示
表示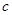 ,并求
,并求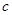 的取值范围.
的取值范围.
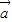 =(-
=(-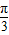 ,-2)平移后得到函数y=cosx的图象.
,-2)平移后得到函数y=cosx的图象.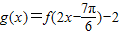 的图象(一个周期).
的图象(一个周期).
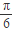 )+α(α∈R).若x∈[0,
)+α(α∈R).若x∈[0,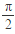 ]时,f(x)的最小值为-2,求α的值.
]时,f(x)的最小值为-2,求α的值.
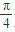 )-1
)-1